Learning the Infinitesimal Generator (IG) of Continuous-Time Markov Processes

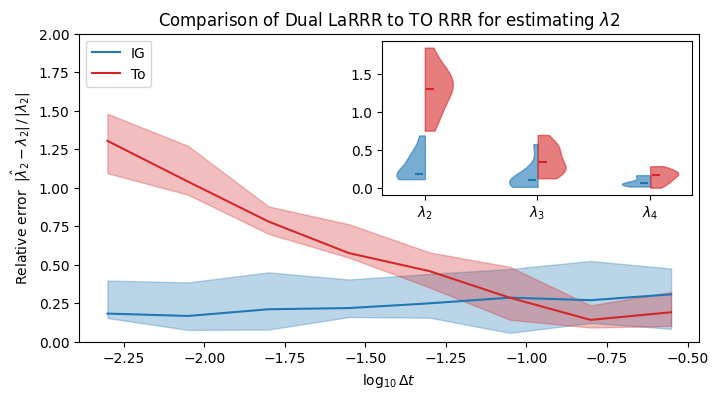
In modeling continuous-time stochastic systems—such as Langevin dynamics—data are typically collected at discrete time intervals $\Delta t$. Although the ultimate goal is to recover the eigenfunctions of the infinitesimal generator $L$, which capture the system’s essential dynamics, researchers often estimate the associated Koopman (or transfer) operator $A_{\Delta t} = e^{\Delta t L}$ instead. This operator shares the same eigenfunctions as $L$, but is simpler to estimate and analyze using standard operator learning methods. However, these methods break down as $\Delta t \to 0$, a regime often required in molecular dynamics to observe fast transient events. In this regime, the spectral gap of $A_{\Delta t}$ collapses: $ gap_i(A_{\Delta t}) \approx \Delta t\, gap_i(L) \to 0$ as $\Delta t \to 0$, even though $gap_i(L) > 0$, which severely degrades the accuracy of spectral estimation. This presents a core challenge: fine time resolution (small $\Delta t$) is needed for modeling fast events, but it undermines the ability to recover meaningful dynamics via $A_{\Delta t}$.
\textbf{Contribution:} To overcome this, we aim to recover $L$, as it governs the underlying continuous dynamics and is independent of $\Delta t$. However, since $L$ is an unbounded operator, direct estimation is challenging. Instead, we estimate its resolvent $\mathcal{R}_\mu = (\mu I - L)^{-1}$ (for some arbitrary complex $\mu$), a bounded—and in many important cases, compact—operator, which shares the same eigenfunctions as $L$.

We propose two approaches:

1. Laplace Reduced Rank Regression (LaRRR). A model-agnostic method based on the Laplace representation

We propose a numerical approximation of the Laplace representation as a weighted sum of RRR estimators of $A_{j\, \Delta t}$, $j\in [J]$ for some $J$ where $A_{ t} f(x) = \mathbb{E}[f(X_{t}) \mid X_0 = x]$ for any function $f \in L^2_{\pi}$. This method is broadly applicable to a large class of processes beyong the self-adjoint case.

2. Physics-Informed Learning via Dirichlet Forms. For time-reversible diffusions with an associated Dirichlet form, we exploit this structure to define a training loss that reflects the underlying physics. When the Dirichlet form is known up to a set of parameters, we propose an efficient estimate from data. This approach leads to faster convergence compared to the agnostic LaRRR method, though it is limited to cases where the generator is self-adjoint and does not scale well to very large systems.